* O melhor site de estudos para Engenharia e Exatas: http://bit.ly/2ALKD9Z* Mais Aulas e Exercícios resolvidos de Mecânica Vetorial: http://bit.ly/2AIIg88—.. Vetor unitário significa que ele tem módulo um. Então, o módulo do produto vetorial escalar são muito próximos. Ambos têm um módulo de ambos os vetores ali, produto escalar, cosseno de teta, produto vetorial, seno de teta. Então, a enorme diferença é que seno de teta tem uma direção, é um vetor diferente que está perpendicular a.
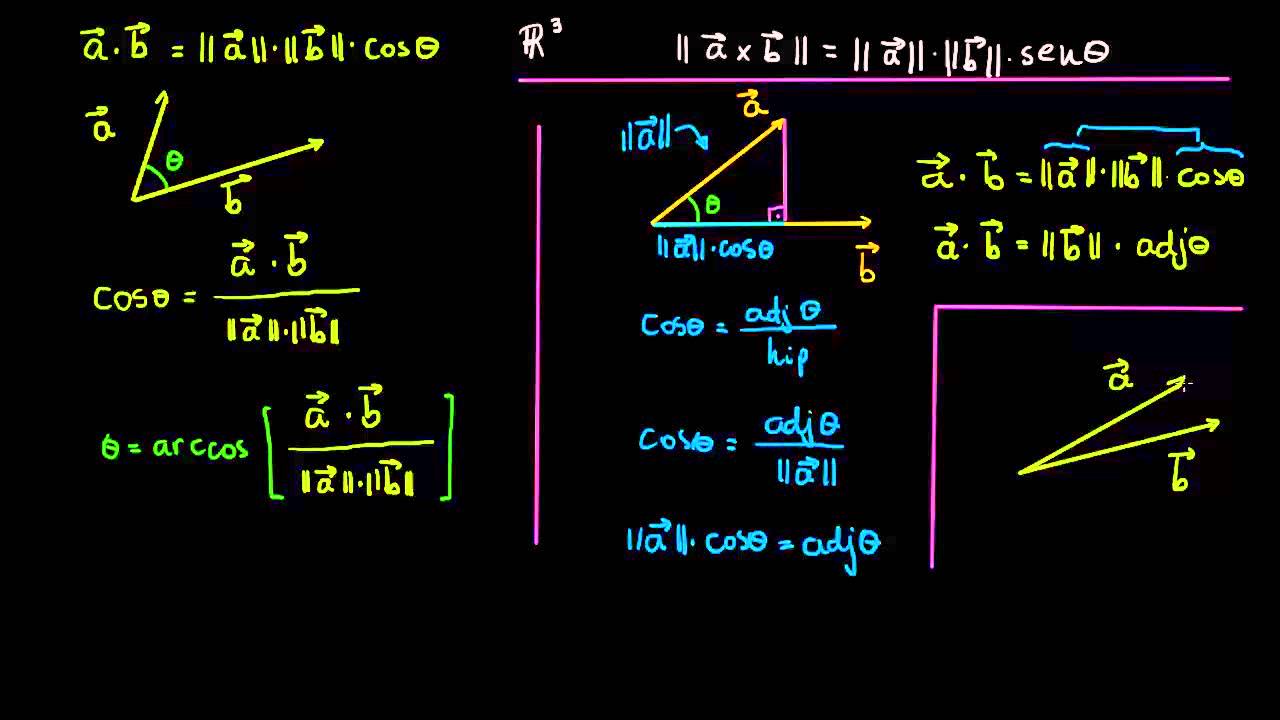
Comparação intuitiva entre produto escalar e produto vetorial YouTube

Qual a diferença entre Produto Escalar e Produto Vetorial YouTube
Produto Escalar Vetores e Produtos Vetoriais

10 Produto vetorial Propriedades YouTube

PPT Introdução à análise Vetorial PowerPoint Presentation, free download ID5585137

Produto vetorial Vs Produto escalar Tudo Sobre Ciências Amino

Vetores soma, produto escalar e produto vetorial com fx991ES Plus2S4DT da CASIO YouTube

CONVENÇÃO DE EINSTEIN Produto Escalar e Produto Vetorial 1 YouTube

Geometria Produto Escalar Vetores YouTube

Produto Escalar, Vetorial, Misto e Aplicações (momento de força, interpretação de determinantes

Vetores no Plano e no Espaço/ Produto Escalar/ Produto Vetorial (assunto completo) YouTube

Produto Vetorial Como calcular? YouTube
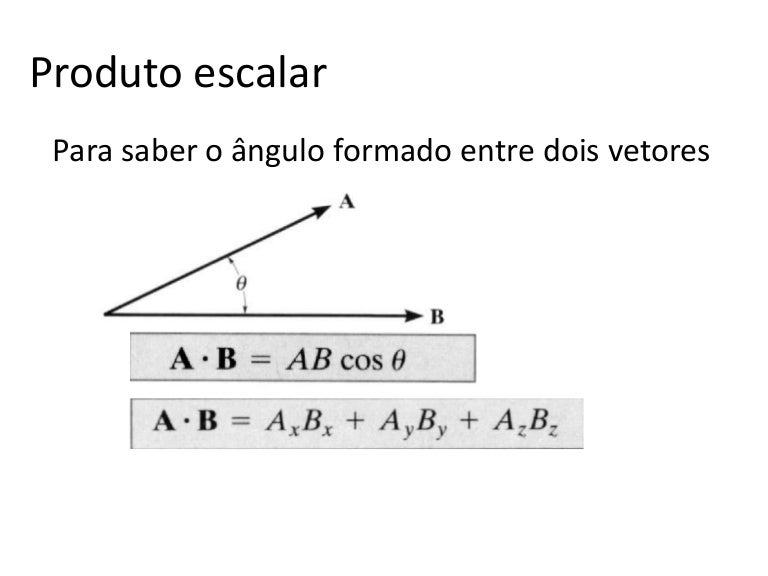
Produto escalar
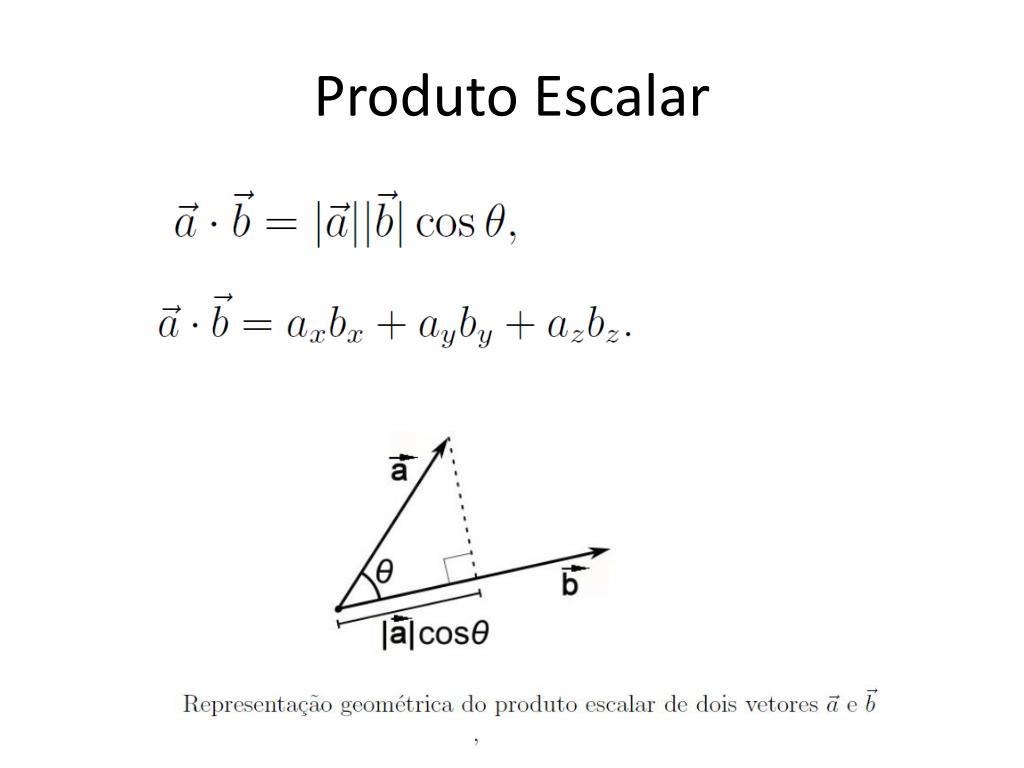
PPT Cálculo vetorial PowerPoint Presentation, free download ID2269029

Produto Escalar Vetores matemática 11.º Ano YouTube
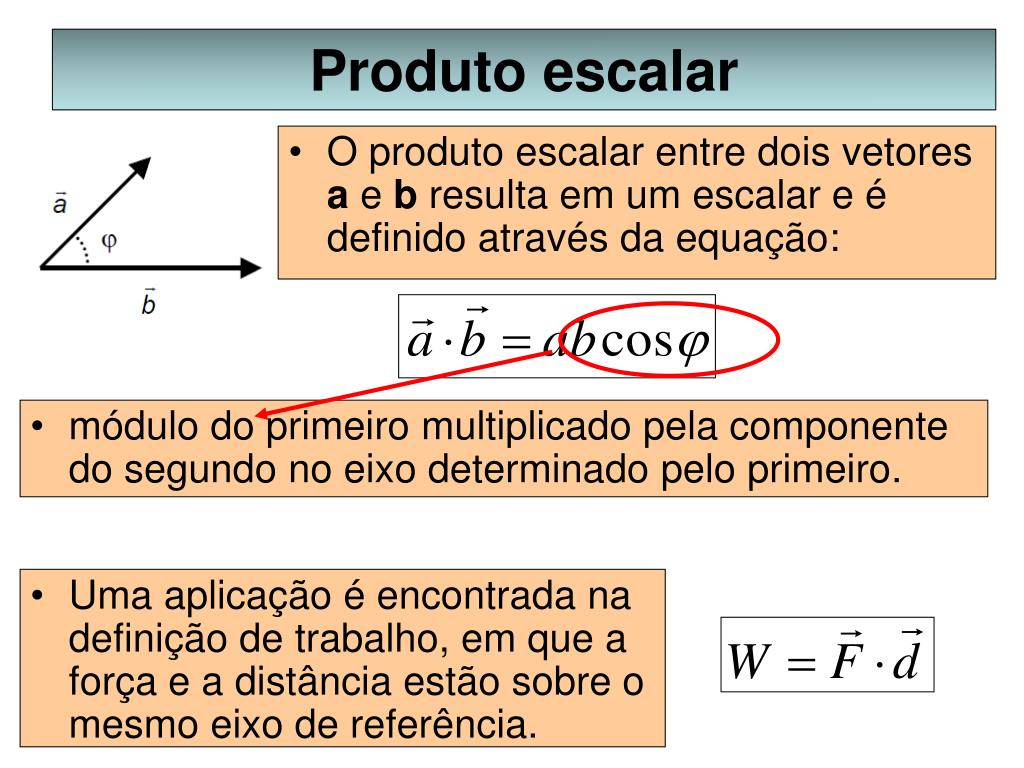
PPT Introdução à análise Vetorial PowerPoint Presentation, free download ID5585137
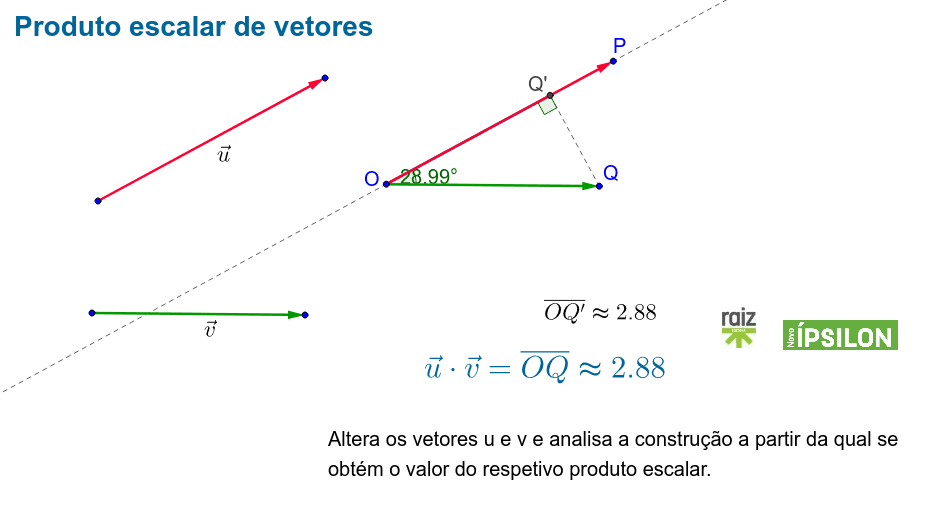
Produto escalar de vetores GeoGebra
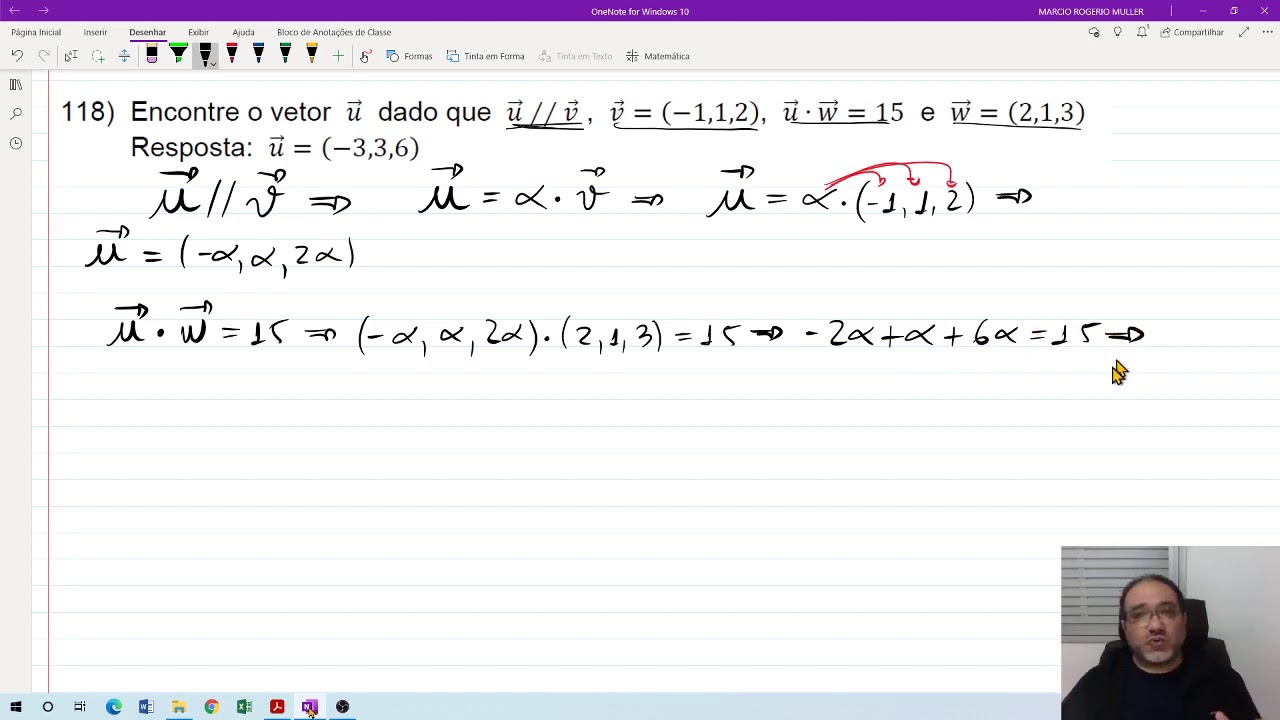
Geometria A. e Á. Vetorial Roteiro 4 (Produto Escalar) Definição e Propriedades ex. 118

Vetores Produto Escalar YouTube
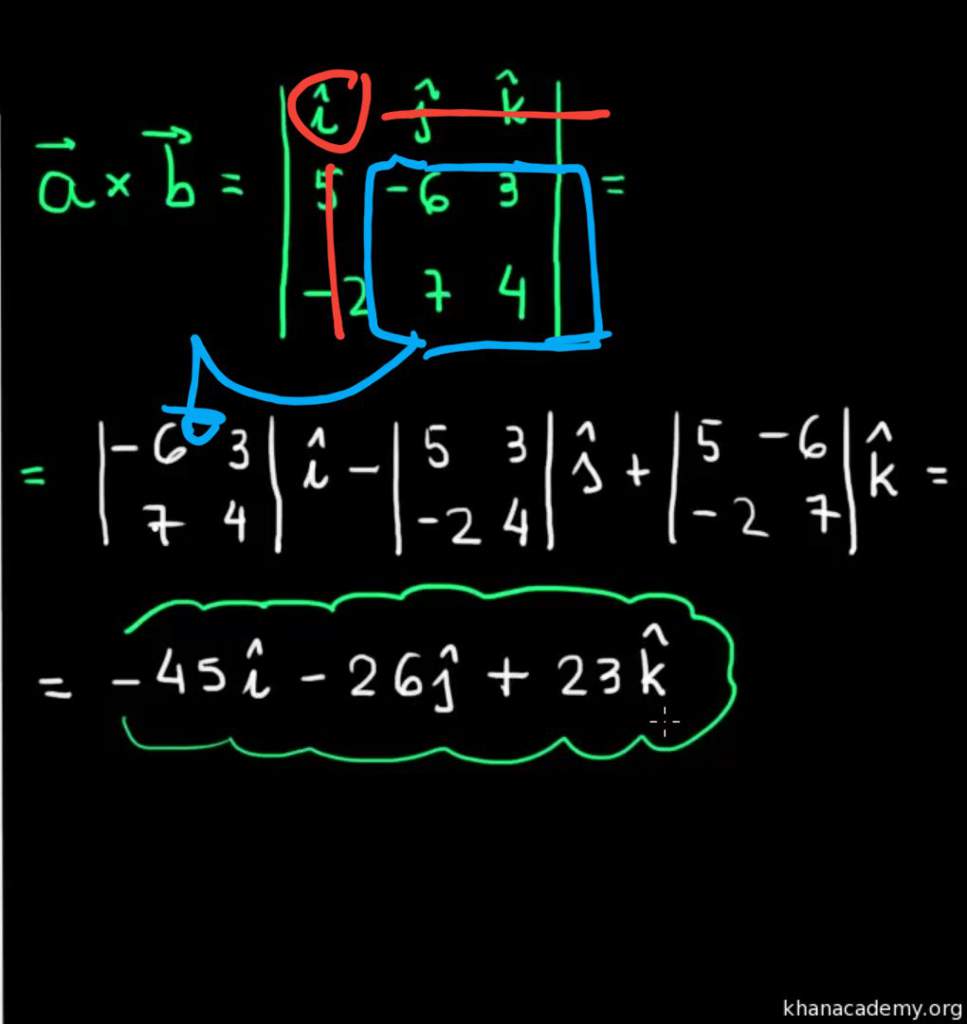
Produto vetorial Vs Produto escalar Tudo Sobre Ciências Amino
Ângulo entre dois vetores. O produto escalar entre os vetores u e v pode ser escrito na forma: u.v = |u| |v| cos (x) onde x é o ângulo formado entre u e v. Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como: desde que nenhum deles seja nulo.. RKA – Neste vídeo vamos estudar algumas propriedades do produto escalar de vetores. E algumas coisas você vai notar muito familiares porque você já usa com os números. Entretanto, nós estamos aqui tratando de vetores, não podemos assumir que nada é verdadeiro sem antes provar. E é o que nós vamos fazer. A primeira coisa que nós vamos.